

Une page entière consacrée à la masse moléculaire? Cela peut sembler étrange, mais la masse moléculaire n'est pas la même pour les polymères et pour les petites molécules. Et nous ne parlons pas seulement du fait que les polymères ont de très hautes masses molaires. Laissez nous vous expliquer:
Prenons une petite molécule, disons l'hexane. L'hexane a une masse moléculaire de 86. Toute les molécules d'hexane ont une masse moléculaire de 86. Maintenant on ajoute un autre carbone à notre chaîne, et la quantité nécessaire d'atomes d'hydrogène, la masse moléculaire passe à 100.

D'accord, mais la molécule n'est plus de l'hexane. C'est de l'heptane! Si on a un mélange de molécules d'hexane et de molécules d'heptane, le mélange ne se comporte ni comme de l'hexane pur ni comme de l'heptane pur. Les propriétés du mélange, comme son point d'ébullition, sa pression de vapeur, etc...ne sont ni celles de l'heptane ni celles de l'hexane.
Mais les polymères sont différents. Imaginez le polyéthylène. Dans un échantillon de polyéthylène certaines chaînes ont cinquante mille atomes de carbone, et d'autres en ont cinquante mille deux, mais cette petite différence ne changera rien aux propriétés. Si vous voulez vraiment savoir la vérité, on ne trouve presque jamais de polymère synthétique dans lequel toutes les chaînes ont la même masse moléculaire. A la place on a une courbe en cloche, une distribution des masses moléculaires. Certaines des chaînes sont beaucoup plus longues que d'autres, à un bout de la courbe. D'autres sont beaucoup plus courtes, à l'autre bout de la courbe. Le plus grand nombre de chaînes est en général situé autour du point central, le point le plus haut de la courbe.
Donc quand on parle des polymères, il faut parler de masse moléculaire moyenne. Et ça ne s'arrête pas là. La moyenne peut être calculée de différentes façons, et chaque façon a son intérêt. Alors parlons de quelques-unes de ces moyennes, d'accord?
La masse moléculaire moyenne en nombre n'est pas trop difficile à comprendre. C'est juste la masse totale de toutes les macromolécules dans un échantillon divisée par le nombre total de macromolécules de l'échantillon.
La moyenne en poids est un petit peu plus compliquée. Elle est basée sur le fait que une molécule plus grosse contient davantage de la masse totale de l'échantillon de polymère qu'une molécule plus petite.
Comparer quelques villes Américaines peut être un bon moyen pour comprendre la différence entre la moyenne en nombre et la moyenne en poids.
Prenons quatre villes, disons Memphis, Tennessee; Montrose, Colorado; Effingham, Illinois; et Freeman, Dakota du Sud. Maintenant jetons un coup d'œil à leurs populations.

Maintenant calculons la population moyenne des quatre villes:
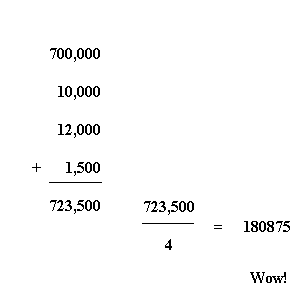
Pour ces quatre villes, la population moyenne est de 180 875 personnes.
Mais on pourrait considérer cela d'une façon différente. Jusqu'à maintenant nous nous sommes occupés de "la ville moyenne". Quelle est la population de "la ville moyenne"? Mais oublions un instant les villes et pensons aux gens. Quelle est la taille de la ville où vit la personne moyenne de ces quatre villes?
Si vous regardez les nombres vous verrez que la personne moyenne ne vit pas dans une ville de 180 000 personnes. La plupart des gens de ces quatre villes vivent à Memphis, qui compte beaucoup plus de 180 000 habitants. Alors comment est-ce qu'on fait pour calculer la taille de la ville où vit la personne moyenne, si la moyenne simple ne marche pas?
Ce qu'il nous faut c'est une moyenne pondérée. C'est une moyenne qui tiendrait compte du fait qu'une grande ville comme Memphis représente un plus gros pourcentage de la population totale des quatre villes que Montrose, Colorado. Faire ceci implique un petit peu de mathématiques qui semblent compliquées mais ne la sont pas. Tout ce qu'on fait c'est prendre le nombre total de gens de chaque ville, et de le multiplier par la fraction de la population totale de cette ville. On prend tous les résultats obtenus pour chaque ville et on les ajoute, et on obtient un résultat appelé population moyenne en poids des quatre villes.
Voyons concrètement ce que ça veut dire. Prenons Memphis. Elle a une population de 700 000 personnes. La population totale des quatre villes est de 723 500. Donc la fraction de la population qui vit à Memphis est ...
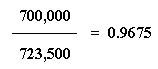
...0,9675, soit 96,75% . Maintenant prenons notre fraction, 0,9675, et multiplions par la population de Memphis:
![]()
Et on obtient 677 273,3. Faisons la même chose pour chaque ville, et additionnons les résultats:

La population moyenne en poids est de 677 600. On peut donc dire que la personne moyenne vit dans une ville de 677 600 habitants. C'est plus crédible que de dire que le citoyen moyen vit dans une ville de 180 000 habitants.
On fait la même chose avec les polymères. On calcule, avec la même formule que celle que l'on a utilisée pour les villes, la masse moléculaire moyenne en poids.
La masse moléculaire peut aussi être calculée à partir de la viscosité d'un polymère en solution. Le principe est simple: les grosses molécules de polymères donnent une solution plus visqueuse que les petites molécules. Bien entendu, la masse moléculaire obtenue en mesurant la viscosité est différente à la fois de la masse moléculaire moyenne en nombre et de la masse moléculaire moyenne en poids. Mais elle est plus proche de la masse moléculaire moyenne en poids. Pour en savoir plus sur la mesure de la masse moléculaire par la viscosité, lisez la page de la viscosimétrie en solution.
Avec toutes ces masses moléculaires moyennes différentes les choses risquent de devenir un peu confuses. De plus, aucune d'entre elles ne peut tout dire à elle seule. Donc il vaut mieux connaître la distribution des masses moléculaires. La distribution est une courbe comme celle de la figure ci-dessous. Sur l'axe x on a la masse moléculaire et la quantité de molécules d'une masse donnée sur l'axe y. Juste pour information, nous vous montrons où se trouvent les masses moléculaires moyennes en nombre, en poids et en viscosité sur la courbe.
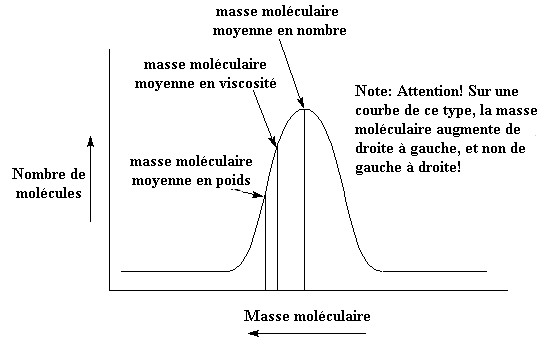
Si nous vivions dans un monde parfait, dans lequel les distributions moléculaires étaient toujours de belles cloches, connaître simplement les moyennes serait suffisant. Mais elles ne sont pas toujours comme ça. Parfois elles sont comme ça:
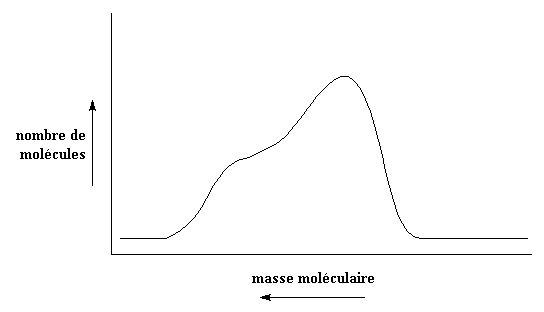
Ce type de distribution résulte de ce qu'on appelle l'effet Tromsdorff, que l'on peut trouver dans les polymérisations radicalaires vinyliques. Quelques fois la distribution est encore plus moche, comme celle ci:
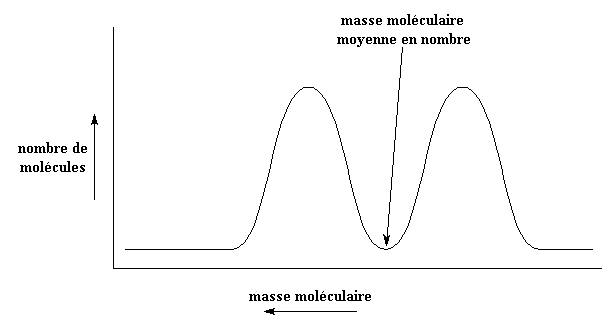
Ici la masse moléculaire moyenne en nombre est un total mensonge! Il n'y a pas une seule molécule de cette masse dans tout l'échantillon! Des cas comme ceux-là illustrent le besoin de connaître la distribution complète. La distribution peut être connue par une technique appelée chromatographie par exclusion de taille, et également par une nouvelle méthode appelée spectrométrie de masse MALDI.
Copyright ©1995,1996 | Department of Polymer Science | University of Southern Mississippi